 타자 스탯
타자 스탯
RC27, 빌 제임스가 발견한 "득점의 본질"
2015-02-12 목, 23:19
By
KBReport
[Baseball Stats Glossary 2]
RC27, 빌 제임스가 발견한 "득점의 본질"
RC/27은 RC:Runs Created 에서 파생된 세이버메트릭스 지표입니다. 타점처럼 누적지표의 성격을 가지고 있는 RC가 타석수가 서로 다른 선수들의 득점생산력을 비교하는데 부적합하기 때문에 이를 보완합니다. RC가 그런 것처럼 RC27 역시 빌제임스가 고안한 지표입니다.
혹시라도 지표의 이름으로 인해, RC27이 RC값을 27로 나누어 구한다는 끔찍한 오해를 하지 말아주시면 좋겠습니다. RC27은 RC에서 그 선수가 당한 [아웃]의 갯수로 나눕니다. 빼앗긴아웃카운트는 대략 출루에 실패한 타석수를 의미합니다.
(wiki 의 RC27 항목에는 벌써 몇년째 RC27 = RC/27 이라는 정체불명의 수식이 그대로 수정안되고 있네요)
개념상, RC27은 그 선수가 “한 경기 모든 타석에 설 경우” 팀이 몇점을 득점할 것인가 라는 스케일입니다. 따라서 한 선수의 RC/27 값은 팀의 경기당 득점과 비교할 수 있습니다. 그런 이유로 리그 경기당 득점이 4.8 일때, 어떤 선수의 RC/27이 5.2 라면 그는 리그평균 이상의 공격력을 가진 선수라는 뜻이 됩니다. 그리고 경기당 득점이 0.1점 높아지면 팀수비투수력이 리그평균이라 할때, 팀의 승률은 5할대비 대략 1푼씩 높아집니다. 이걸 계산하면 그 선수가 평균수준의 타자에 비해 팀에게 시즌 몇승을 추가로 선물하는지 알 수 있습니다. 대체레벨이 다를 뿐 WAR를 계산하는 원리도 같습니다.
계산방법은 다음과 같습니다.
(일반적인 계산방법)
RC27 = RC / (At bats타수 - H안타 + CS도루실패 + SH희생번트 + SF희생플라이 + GIDP) * 27
(좀더 엄격한 계산방법)
RC27 = RC / (3*리그전체아웃카운트/리그 팀 경기수) / OutsMade
where OutsMade = At bats타수 - H안타 + CS도루실패 + SH희생번트 + SF희생플라이
(좀더 간단한 계산방법 RC25)
RC/25 = RC / O * 25
A = H + BB - CS
B = TB + .64 * SB + .24 * BB - .03 * K
C = AB + BB
RC = A * B / C
O = AB - H + CS
OutsMade를 계산하는 원칙은 다음과 같습니다. 타석에서 당한 아웃, 루상에서 당한 아웃, 자신의 책임으로 주자를 죽은 아웃. 이렇게 4가지가 고려됩니다.
1. [타수]에서 안타H를 제외합니다. 단 사사구는 제외하지 않습니다. 왜냐하면 타수에는 이미 사사구 숫자가 제외되어 있기 때문입니다.
2. CS도루실패 를 제외합니다.루상에서 당한 아웃이기 때문입니다.
3. GIDP병살타를 제외합니다. 자신도 죽었지만 자신의 책임으로 주자도 죽여서 아웃카운트가 늘어났기 때문입니다.
4. SH, SF를 더합니다. 타수에서는 희생번트와 희생플라이가 제외되어 있었는데 어쨌든 희타와 희플은 아웃카운트를 빼앗긴 것이기 때문에 여기서는 포함시킵니다.대신 RC에 이미 희타와 희플의 플러스 가치가 계산되어 있기 때문에 공평합니다.
27을 곱하는 이유는, 한 경기 아웃카운트가 27개이기 때문입니다. 즉 27번 아웃당하는 동안 이 타자가 몇점의 득점을 만드느냐 계산하고 있는 것입니다.
좀더 엄격한 계산방법이 약간 다른 이유는, 야구가 일반적으로 27개의 아웃카운트로 끝나긴 하지만 연장전에 있어서 항상 그런건 아니라서 만들어둔 것 같습니다. 이런 것들 볼 때마다 세이버메트리션들이 통계를 대하는 엄격함에 놀랍니다. 동시에 이런 엄격함의 반대 측면에서 좀더 쉽게 구할 수 있는 데이터를 가지고 좀더 간편하게 해당 지표를 큰 오차 없이 계산할 수 있는 보급형 지표를 빼놓지 않는 섬세함과 친절함도 가지고 있습니다.
RC27의 보급형 버전 RC25
그 결과물이 RC27의 보급형 버전인 RC25 입니다. RC25는 AB, H, BB, TB루타수, K삼진, SB, CS 만으로 계산할 수 있습니다. 당시만 해도 그 이외의 SH, SF, GIDP, HBP, IBB 심지어 PA타석 기록을 제공하지 않는 경우가 많았을 겁니다. 특히 빌 제임스가 고안한 지표들에게 이런 친절함을 자주 발견하는데, 그가 세이버메트릭스를 대중적으로 확산시키는데 가장 결정적인 역할을 했다는 게 우연은 아닌 거 같습니다.
RC에서 RC2002 버전이나 RC_Technical 버전이 아니라 RC_Basic 버전으로도 비교적 비슷한 RC값을 계산해 낸다는 것을 확인한 바 있습니다. RC25 역시 괜찮은 정확도를 가지고 있습니다.
세이버매트리션들은 야구통계를 다룰 때 별스러울만큼 엄격함을 추구합니다. 그러나 그것은 “야구에 대한 더 객관적인 지식”을 추구하기 위함이며 편견과 관습, 왜곡된 기억으로부터 올바른 지식을 찾아내기 위함입니다. 자세한 기록을 찾아내고 확인할 수 없는 팬들, 복잡하고 어려운 계산을 해내기 부담스러워하는 사람들을 배제하거나 무시하기 위해서가 아닙니다.
그리고 실제로 그들이 세이버메트릭스라 불리는 이 새롭고 혁신적이며 매력적인 야구의 지평 안에 기꺼이 참여할 수 있도록 노력합니다. 그래서 충분한 객관성과 엄격함을 여전히 유지하면서도 더 쉽게 활용할 수 있는 [보급형 계산모델]을 함께 만들어냅니다.
컴퓨터와 같은 성능좋은 계산도구를 사용할 수 없다는 이유로 그들이 이 즐거움에서 배제되어야 합니까? 애당초 빌제임스 자신이 종이와 연필 그리고 기껏 탁상용 계산기로 이 모든것을 이루어냈다는 것을 기억할 필요가 있습니다. 그리고 다른 이들에게도 그런 즐거움을 기꺼이 나누기 위해 애썼다는 것을 생각해볼 필요가 있습니다.
RC나 RC27은 예전에 비해서는 많이 사용되는 편은 아닙니다. 그보다 좀더 나은 다른 지표들이 만들어졌기 때문입니다. 숫자0 을 발명해낸 어떤 아라비아인이나 (인도인인가요?) 미지수x를 발명해낸 어떤 유럽인이 수학에 끼친 영향에 비견될, 톰 탱고의 24PA혁명 이후 더 명료하고 정확한 다른 계산모델이 고안되었으며 컴퓨터와 스프레드시트 같은 계산도구의 확산, 아주 세부적인 지표까지도 쉽게 손에 넣을 수 있는 인터넷 환경 이 모든 것의 영향 때문일 겁니다.
빌제임스가 발견한 법칙, [득점=출루*진루]
하지만 세이버메트릭스에 흥미가 있다면 빌제임스의 RC와 RC27에 대해 관심을 가질 이유는 아직도 충분합니다.
330년 전의 한 영국인은 천체와 사물의 움직임을 꿰뚫어 [힘 = 질량 * 가속도]라는 법칙을 찾아냈다면, 빌제임스는 야구라는 또 다른 우주의 비밀을 들추어 [득점 = 출루 * 진루]라는 원리를 발견했습니다. 물리학과 야구 어느 것이 더 중요한지는 사람마다 다르게 느끼겠지만, 야구에 대한 그의 섬광같은 통찰의 가치를 감히 우주에 대한 뉴튼의 발견에 비한다면 --- 음 그건 좀 과하긴 하네요. 흠흠.
어쨌든 복잡성 뒤에 그리고 "야구 몰라요"라는 격언 뒤에 가려져 있던 야구의 본질에 대해 빌제임스가 밝혀 증명한 득점의 법칙 [득점 = 출루 * 진루]라는 RC:Runs Created 의 통찰은 더없이 아름답고 위대합니다. 그리고 또 하나, 당시의 야구기록 통계의 현실적 제약들, 아마도 새로운 지표에 관심을 가질 법한 야구팬들의 현실적 한계를 습관처럼 배려했던 그의 철학을 RC 라는 지표를 통해 엿볼 수 있습니다.
세이버메트릭스의 가치는 흔한 그러나 슬픈 오해와 달리 콤마 단위로 선수를 평가해서 줄세우는데 있지 않습니다. 그들은 그런 목적을 위한 엄격함과 정밀함을 추구한 적도 없습니다. [통계]라는 도구 속에는 어쩔 수 없는 오차가 늘 내재되어 있기 마련이며 그래서 진짜 세이버메트리션들은 그런 오차의 여지를 명확히 밝혀 스스로의 한계를 긋는데 더 열심입니다.
그들이 추구하는 엄격함과 정밀함은, 편견 그리고 부정확한 기억력으로부터 자유롭기 위함입니다. 그리고 무엇보다 야구를 좀더 즐겨보자는 것입니다.
Appendix. KBO14시즌, RC27 Top30
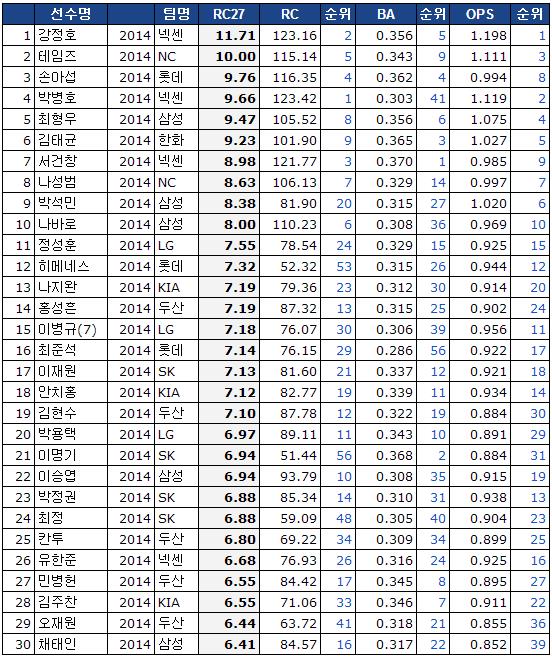
RC가 누적스탯에 가까운 구조인 것과 비교해서 RC27은 비율스탯에 가깝습니다. 따라서 RC의 순위와 RC27의 순위가 일치하지 않는 것은 당연합니다. 비슷한 RC를 가지는 선수가 있다면 그중 타석수가 작은 타자의 RC27이 더 높습니다. RC에서 1위였던 박병호는 RC27에서는 4위로 내려앉습니다. 대신 강정호가 1위에 오릅니다.
타율BA의 순위와 일치하지 않는 것은 [타율]이라는 지표가 타자의 득점생산성을 측정하는데 부족하다는 것을 잘 보여줍니다. [타율]에 비해 득점생산성을 좀더 잘 설명하는 [OPS]와 비교한다면 RC27의 순위는 OPS의 순위와 대체로 비슷한 경향을 보입니다. 다만 OPS는 출루율에 비해 장타율을 과대평가하는 성향이 있기 때문에 비슷한 수준의 OPS를 기록하면서 출루율이 상대적으로 높은 타자들의 RC27이 더 높게 측정됩니다. 손아섭, 정성훈, 나지완, 홍성흔 등이 OPS에 의해서 과소평가되는 선수들입니다.



 타자 스탯
타자 스탯

